Photo by DDP on Unsplash

With so many iOS architectures out there these days, I was sure that one would speak to me. I’ve tried Viper, MVVM, ReSwift and others. They each had their merits but ultimately their shortcomings prevented me from using them. So what did I do?? I Invent one more architecture! And what is the worst name I could come up with for it? Glad you asked! I call it “Yet Another iOS Archtecture” or YAIA (pronounced ‘Yay-yeah!’).

Goals of YAIA

An architecture should have goals, otherwise its just a collection of arbitrary rules which is no fun. Below I’ll describe some of the values that motivated YAIA.

1. Writing unit tests should be painless. This is the main goal of YAIA and everything else falls out of that. I’d like to write test without mocks, fakes or injecting anything. I’d like to avoid testing async code and I certainly don’t want to do any IO such as reading files or hitting a database in my tests. I’d like my test to run as quickly as possible.

2. The architecture should be flexible and light weight. It doesn’t require implementers to create classes X, Y and Z and protocols for each of those classes (I’m looking at you, Viper!). I also don’t want tests to implement stubs or mocks to facilitate testing.

3. Changes should be easy to make. This is related to points one and two. I don’t want to discourage users from making improvements because it will require changes in many places or might break something.

4. Simple. No unnecessary abstractions or classes. Abstractions such as protocols or base classes can make your code flexible but they also make it harder to follow. Every class or protocol has to earn its place. If it doesn’t, it’s out.

To achieve these goals, I cherry-picked features from a few different architectures I had used in the past. From ReSwift, an implementation of the redux pattern, I borrowed its emphasis on value types and keeping data and logic in one place. In YAIA, the models that represent the business and app logic are all value types (as opposed to reference types). The inputs and outputs to this values-only system are also values. This makes results easy to verify by simply making them Equatable. A nice side effect of a values only system is that it’s impossible for it to contain any async code paths (a struct or other value type can’t be captured by reference in an escaping closure). This keeps tests simple and running fast.

While there are many things to dislike about Viper, one of its tenants is that services should be hidden behind interfaces. This is one place where an abstraction can be nice. Types from services shouldn’t creep into the business logic. What this means for iOS is that Core Data’s NSManagedObjects, wont be referenced in the values-only core. Instead, we copy data out of Core Data and into plain old Swift structs. These value type are then passed into our system. This allows us to test our system without instantiating Core Data objects. It also means that I can switch persistence technology without too much pain since the Core Data dependencies are contained; our business logic layer will be unaffected when we change the type of database we’re using.

A brief overview

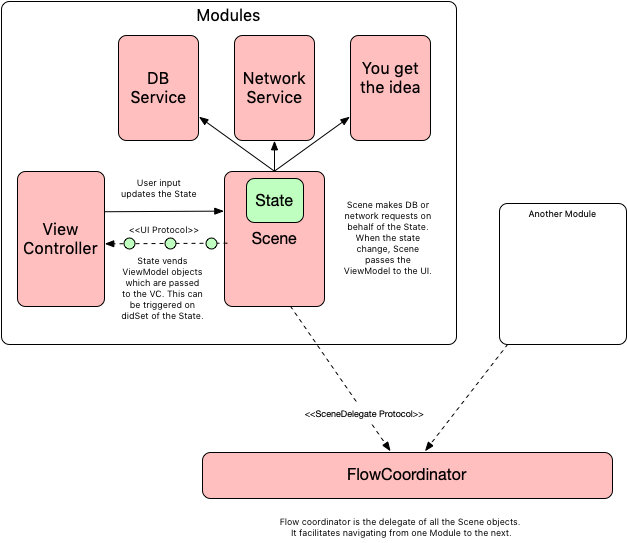
I’ve described this architecture in previous posts but I’ll go over the highlights here. For a given screen you’d like to build, a login screen perhaps, the class that ties the different elements together is called a Scene (naming things is hard). In this simple example of a login screen I’ve called it LoginScene. It behaves similarly to the ViewModel in MVVM. In YAIA, it has a weak reference to the view controller via a protocol. This is one of the few places that I use a protocol in YAIA. The view controller has a strong reference to the Scene so that the Scene’s lifecycle is tied to the view controller’s.

The Scene object contains a State object which is some sort of value type; generally a struct or enum. I will discuss the State object further but for now understand that the bulk of the logic resides here. The Scene object may also have network or database services as dependencies. The Scene’s job is to move data between the State object and these dependencies (the UI is also a dependency).

It is the Scene’s responsibility to take input from the UI, a button press for instance, and pass it to the State object for processing. At this point, the State object might update its internal state and possibly return a value type indicating the IO to be performed. The Scene would then tell the appropriate interface to perform the request (eg network request). The result of this request is then fed back into the State for processing. If the State object determines a view transition is required, it will return an enum representing that transition which is then passed to a flow coordinator which handles the transition.

To update the UI, the State will return a ViewModel instance which is passed to the ui by the Scene. In YAIA, a ViewModel is a simple data transfer object (a value type of course) that contains all the info the view needs to update itself with.

But how does all this help me?

How does YAIA achieve the goals listed above? Since the main goal is to make software testable, I had to figure out what type of code is easily tested. I discovered that if you separate the logic and state from the IO, the state/logic portion becomes much more testable. The easiest thing in the world to test is a function that takes values in and returns a value. I wouldn’t hesitate to write a test for func add(a: Int, b: Int)->Int. It takes values as inputs and returns a value. It doesn’t have any internal state, doesn’t read from a database and doesn’t have any dependencies that make the tests complicated. A test based on this method would be easy to read and debug.

The opposite end of the spectrum is a class which handles all of its IO internally and has its logic and IO coupled together. This class may be dependent on other complex classes which must be recreated in a test environment or mocked. When testing this code, the setup ends up being many times longer than the actual test and verification portion of the test. This means the tests are brittle and hard to read. Additionally, since they take so much effort to configure, developers will be less inclined to write tests in the first place. By making the State object a value which doesn’t do any IO, we side step most of the difficulties above.

To achieve flexibility, I recommend using your best judgment regarding when to use the pieces above. If you’re building a screen with some text and a single button, put all the logic in the view controller and move on. This is just one approach to separating logic from IO but there are other ways to achieve the same goal. When it comes to architecture, one size does not fit all.

In the end, the specific names of the components and the exact responsibilities of a given class don’t matter. What matters it being able to write software that is easily verified by unit test. This is achieved by isolating logic in value types and away from the async code and IO. By doing that, you are one step closer to making tests work for you.

I'm a freelance iOS developer based in San Francisco. Feel free to contact me.

✎ Edit post